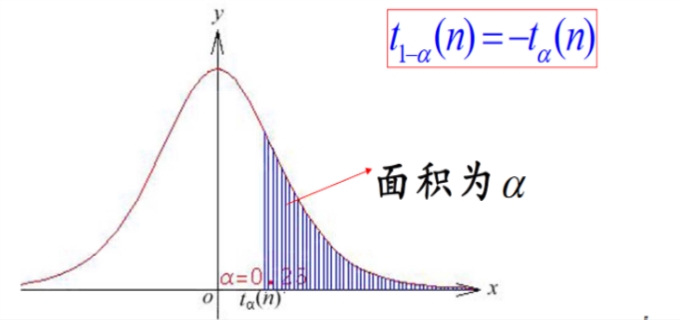
1.分位数意义是表示了在这个样版集中。从小至大排列之后。小于某值样版子集约为样本集占比。分位数回归思想的提出到现在已经有近30多年了，经过这近30多年的发展，分位数回归在理论与方法上都日趋成熟，并广泛用于多种课程中。它对实际问题能提供更全面的分析,无论是线性模型或是非线性模型，分位数回归都是一个非常好的工具，它对一般线性回归模型做了有益的补充。
2.分位数回归法的独特情况是中位值重回(最小一乘重回)，用对称权重解决残差小化难题，而其他条件分位数回归则要用非对称加密权重解决残差降到最低。
分位数如何计算
相关文章
猜你喜欢
- 免高考读大专？2025高职单招院校全攻略 2025-06-24
- 什么样的孩子适合报强基计划？2025年竞赛生报考优势分析 2025-06-24
- CPA考试科目有哪些？2025年零基础通关搭配指南 2025-06-24
- 一诺千金起源揭秘，季布如何用诚信改写命运？ 2025-06-24
- 强基计划校测解析，15%分值如何拉开差距？ 2025-06-24
- 碱石灰主要成分揭秘：75%氧化钙如何吸收二氧化碳？ 2025-06-24
- 公立还是民办？国际班学费对比，3年省15万攻略 2025-06-24
- 女生选专业避坑指南：口腔医学起薪8K的就业真相 2025-06-24
- 季风肆虐农业怎么办？3招减灾增产技巧揭秘 2025-06-24
- 胡思乱想停不住？一招让大脑安静下来的技巧 2025-06-24
评论列表 共有 0 条评论
发表评论 取消回复